Bootstrap Confidence Intervals for Standardized Solution in lavaan

R
lavaan
bootstrapping
confidence-intervals
semhelpinghands
standardized
Author

Shu Fai Cheung

Published

September 28, 2022

lavaan supports bootstrap confidence intervals for free and user-defined parameters. This is useful especially for parameter estimates that may not be approximately normally distributed unless the sample size is very large.

However, it is known, though not well-known enough in my opinion, that, even if bootstrap confidence intervals are requested, the confidence intervals reported in the standardized solution are not bootstrap confidence intervals as in tools like PROCESS for standardized effects like standardized indirect effects, but are symmetric delta-method confidence intervals based on the bootstrap sampling variance-covariance matrix.

Let’s use a sample dataset for illustration:

# Create the data
set.seed(860541)
n <- 100
x <- rnorm(n)
m <- .4 * x + rnorm(n, 0, sqrt(1 - .3^2))
y <- .4 * m + rnorm(n, 0, sqrt(1 - .4^2))
dat <- data.frame(x = 10 * x, m = 2 * m, y = 3 * y)

We specify a simple regression model:

library(lavaan)
This is lavaan 0.6-13
lavaan is FREE software! Please report any bugs.
mod <-
"
m ~ a * x
y ~ b * m + cp * x
ab := a * b
"

… and fit it with bootstrap confidence intervals (2023-01-28: Code and results updated for lavaan 0.6-13, iseed is used instead of set.seed()):

fit <- sem(mod, data = dat, fixed.x = FALSE,
           se = "boot", bootstrap = 2000,
           iseed = 8970)

Let’s focus on the confidence intervals of the indirect effect:

est <- parameterEstimates(fit)
std <- standardizedSolution(fit)
# Unstandardized
est[7, ]
  lhs op rhs label   est    se     z pvalue ci.lower ci.upper
7  ab := a*b    ab 0.025 0.015 1.686  0.092    0.001    0.059
# Standardized
std[7, ]
  lhs op rhs label est.std    se     z pvalue ci.lower ci.upper
7  ab := a*b    ab   0.088 0.049 1.774  0.076   -0.009    0.185

They lead to different conclusions.

As shown below, the confidence interval of the unstandardized indirect effect is percentile confidence interval that is asymmetric, as expected:

est[7, c("ci.lower", "ci.upper")] - est[7, "est"]
     ci.lower   ci.upper
7 -0.02364024 0.03392409

However, the confidence interval of the standardized indirect effect is symmetric:

std[7, c("ci.lower", "ci.upper")] - std[7, "est.std"]
     ci.lower   ci.upper
7 -0.09699904 0.09699904

This behavior has been discussed in the Google group forlavaan and so is known, but not “well-known” because I met many users who were not aware of this, especially when they use bootstrapping to get the confidence intervals for indirect effects but found that the confidence intervals of unstandardized and standardized indirect effect led to different conclusions, as in the example above.

A solution already exists in lavaan. Users can use bootstrapLavaan() and get the bootstrap confidence intervals for many results, including the output of standardized solution.

We first define a function to extract the standardized indirect effect:

fct <- function(fit) {
    lavaan::standardizedSolution(fit)[7, "est.std"]
  }

We then update the fit object to disable standard error because we only need the point estimates and then call bootstrapLavaan():

fit0 <- update(fit, se = "none")
fit_boot <- bootstrapLavaan(fit0, R = 2000, FUN = fct, iseed = 8970)

The percentile confidence interval can then be formed by quantile().

(Note that lavaan() does not use quantile() but use the approach by boot.ci(). The resulting interval can be slightly different from that by quantile().)

quantile(fit_boot[, 1], c(.025, .975))
       2.5%       97.5% 
0.004372947 0.196203435

However, this is inconvenient because we need to write custom function, and bootstrapping was done twice unless we store both the unstandardized and standardized solutions in the custom function used when calling bootstrapLavaan().

I wrote the function standardizedSolution_boot_ci(), available in the package semhelpinghands, for this particular case that I sometimes encounter:

This would be useful to me because some of my projects involve large samples with missing data. and bootstrapping takes appreciable time even with parallelization.

This is how to use this function:

library(semhelpinghands)
std_boot <- standardizedSolution_boot_ci(fit)
# -c(9, 10) is used to remove the delta-method CIs from
# the printout
std_boot[, -c(9, 10)]
  lhs op rhs label est.std    se      z pvalue boot.ci.lower boot.ci.upper
1   m  ~   x     a   0.232 0.105  2.213  0.027         0.015         0.425
2   y  ~   m     b   0.379 0.083  4.541  0.000         0.204         0.541
3   y  ~   x    cp   0.103 0.092  1.117  0.264        -0.079         0.281
4   m ~~   m         0.946 0.048 19.527  0.000         0.819         0.999
5   y ~~   y         0.828 0.073 11.403  0.000         0.660         0.940
6   x ~~   x         1.000 0.000     NA     NA            NA            NA
7  ab := a*b    ab   0.088 0.049  1.774  0.076         0.004         0.196

The boot.ci intervals are “true” bootstrap confidence intervals, formed from the bootstrap estimates. The bootstrap confidence interval for the standardized indirect effect ([0.004, 0.196]) and that for the unstandardized indirect effect ([0.001, 0.059]) now lead to the same conclusion.

standardizedSolution_boot_ci() works like standardizedSolution(), but extracts the stored bootstrap estimates, get the standardized solution from each set of estimates, and use them to form the bootstrap confidence intervals for the standardized solution.

By default, the bootstrap standardized solution is also stored in the attribute boot_est_std. They can be extracted to examine the distribution. For example, the bootstrap standardized indirect effects can be extracted and plotted:

std_boot_est <- attr(std_boot, "boot_est_std")
std_indirect_boot_est <- std_boot_est[, 7]
hist(std_indirect_boot_est)

qqnorm(std_indirect_boot_est)
qqline(std_indirect_boot_est)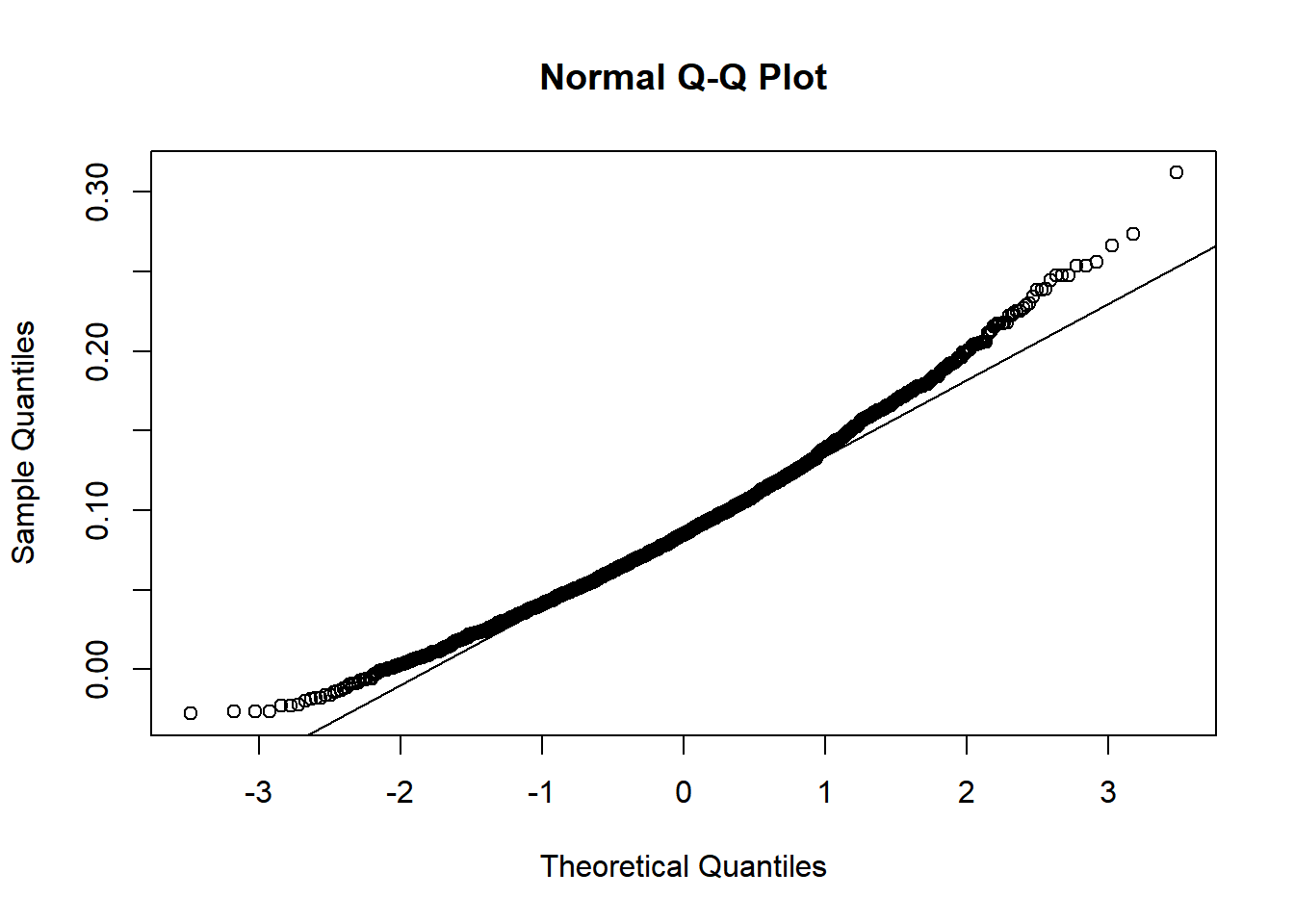

This function is simple to use, at least for me. No need to write custom function, and no need to do bootstrapping twice. In most cases, I don’t even need to specify any additional arguments.

More about this function can be found in the vignette for standardizedSolution_boot_ci().

If any bug in standardizedSolution_boot_ci() was found, I would appreciate submitting it as a GitHub issue. {{< emoji ":smile:" >}}

:::